Il sistema cronologico newtoniano: le applicazioni astronomiche e antiquarie

Il principale merito che si deve attribuire al sistema cronologico newtoniano è senza dubbio l’applicazione, mai tentata prima, del fenomeno, già noto a Ipparco, della precessione degli equinozi, nel tentativo di datare gli eventi storici. Nel terzo libro dei Principia, Newton affronta il problema dell’“aberrazione delle stelle fisse”, cioè della precessione, e ne calcola lo spostamento in 50” 00”’ 12”” all’anno, ovvero circa un grado ogni settantadue anni.[2] L’intenzione di Newton è di collezionare osservazioni antiche e confrontarle con quelle di astronomi suoi contemporanei: avendo a disposizione le posizioni rispetto alle stelle fisse di due solstizi, relative a due diversi momenti, sarà possibile calcolarne la distanza in gradi nella sfera celeste e ottenere quindi la misura del tempo trascorso tra le due osservazioni.
    Newton utilizzò le misurazioni delle posizioni celesti delle stelle fisse relative alla sua epoca effettuate da John Flamsteed (1646-1719), ottenute con l’ausilio del grande quadrante murale dell’osservatorio reale di Greenwich. Le osservazioni risalgono al periodo tra novembre 1689 e gennaio 1690 e furono pubblicate in edizione definitiva, peraltro senza l’esplicita autorizzazione dello stesso Flamsteed, nel 1714.[3] Questione molto più complessa si dimostrò, invece, il recupero di osservazioni utili a stabilire la posizione di un solstizio o di un equinozio in epoche antiche. Newton si dovrà affidare alle vaghe descrizioni degli autori greci e a inevitabili congetture su alcune testimonianze indirette.
    Leggendo Clemente di Alessandria,[4] che come già segnalato è uno degli autori da lui più apprezzati, Newton ritrova in un frammento della Titanomachia, di autore sconosciuto, l’attribuzione al centauro Chirone della realizzazione delle costellazioni. Nella visione evemeristica del mito greco, Chirone veniva considerato un personaggio storico realmente esistito, dedito all'astronomia pratica e all'astrologia,[5] e che avrebbe delineato le σχήματα ολύμπου, ovvero “le figure dell’Olimpo”, qui da Newton interpretate come sinonimo di “asterismi”, come d’altronde sembra fare anche lo stesso Clemente di Alessandria. Tramite, poi, Diogene Laerzio[6] individua Museo come il primo a realizzare (nell’originale inglese, made) una sfera celeste[7] tra i Greci: Newton utilizza il verbo to make, traducendo il generico termine latino fecisse, tradotto a sua volta da Tommaso Aldobrandini (di cui Newton possedeva l’edizione latina delle Vitae), dall’originale greco ποιησαι, precedentemente reso da altri interpreti sia con invenisse (Ambrogio Camaldolese, Carli), che attribuirebbe a Museo il solo merito di aver rinvenuto la sfera, sia con scripsisse (Marco Meibomio, Menagio), che invece considererebbe la sfera un’opera originale dello stesso. Nonostante le incertezze, Newton prende per certa l'attribuzione e, in questo modo, può collocare la prima realizzazione della sfera celeste al tempo della spedizione degli Argonauti (evento che non dubita essere storico), essendo Museo il maestro di Orfeo, che appunto vi partecipò. A conferma di ciò, Newton sostiene il fatto che tutte (tranne due)[8] le costellazioni della sfera, raccontino i miti coevi o precedenti al viaggio di Giasone e i suoi compagni: essa non poteva, quindi, che essere stata realizzata al tempo di quella spedizione, essendo uno strumento per la navigazione in alto mare, tentata per la prima volta dai Greci con una grande nave Argo. Fino a quel momento l'unico metodo di navigazione da loro praticato (sostiene Newton probabilmente tramite la lettura di Plinio)[9] si riduceva alla navigazione di cabotaggio su piccole imbarcazioni. Al ritorno, gli Argonauti sarebbero approdati presso l'isola dei Feaci, Corcira, come indicato dallo Pseudo-Apollodoro,[10] e avrebbero fatto conoscere la sfera a Nausicaa, figlia del re dei Feaci, che infatti è da quel popolo considerata l'inventrice della σφαίρα;[11] ma l'equivoco in cui Newton cade, in questo caso, denuncia una notevole ingenuità: il termine greco riportato aveva presso i Greci il più comune significato di palla da gioco, come si evince, tra gli altri, dal passo omerico dedicato alla stessa Nausicaa.[12]
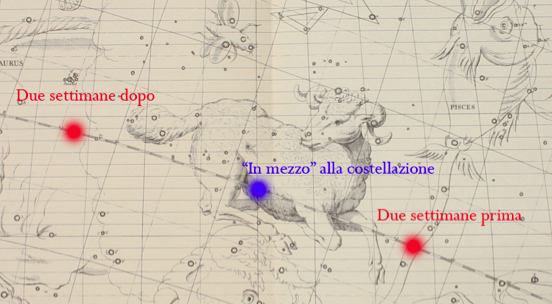
    Stabilito questo, Newton considera che, all'epoca della prima sfera (descritta in séguito da Eudosso e da Ipparco)[13] e quindi della spedizione degli Argonauti, i punti cardinali degli equinozi e dei solstizi si trovassero "nel mezzo" delle costellazioni dell'Ariete, del Cancro, dello Scorpione e del Capricorno. Ciò perché l'antico calendario lunisolare, che considerava l’anno solare diviso in dodici mesi lunari di ventinove giorni più un mese intercalare, poteva cominciare ad ogni ciclo in giorni differenti, ma che al massimo potevano variare di due settimane prima e due dopo l’equinozio primaverile; per evitare che la posizione del Sole, al principio del nuovo anno, sconfinasse nelle costellazioni precedenti o successive, che sono ampie mediamente 30°, i primi realizzatori della sfera posero le costellazioni in modo che i rispettivi equinozi e solstizi (ovviamente con una certa approssimazione e tenendo conto che i dodici asterismi delle costellazioni zodiacali non hanno le medesime configurazioni e la stessa ampiezza) si trovassero nel loro centro, cosicché il massimo sfasamento possibile tra la posizione del Sole e l’inizio del nuovo anno non superasse mai i 15° circa (Immagine 1).

 

 
Newton procede poi con l'individuare il punto mediano tra Prima Arietis[14] e Ultima Caudae Arietis[15] e ne esegue la proiezione sull'eclittica, presumibilmente per via trigonometrica.[16] Il risultato ottenuto, riferito alle coordinate del 1689 (anno delle osservazioni di Flamsteed), è 6° 44' in longitudine eclitticale, cioè 36° 44' dal punto vernale, posizione in cui si trovava il Sole solstiziale al tempo della sfera originaria, secondo le premesse newtoniane già accennate (v. Immagine 2). L'arco di spostamento dovuto alla precessione equivale a 2645 anni (72 anni per ogni grado) e colloca la spedizione degli Argonauti al 955 a.C.
    Con metodo di computo differente, Newton, attraverso la descrizione delle stelle, sempre derivata da Eudosso, presso le quali passavano i coluri equinoziali e solstiziali,[17] ottiene le cinque rispettive posizioni degli astri di riferimento e le proietta nuovamente sull'eclittica; partendo poi dai cinque risultati calcola la loro media aritmetica, con la quale ottiene la posizione del punto equinoziale diversa da quella risultante dal precedente procedimento ma sovrapponibile:  6° 29’ (vedi Tabella I). Un valore che corrisponde a 2627 anni e che colloca la spedizione degli Argonauti nel 937 a.C. (data che prenderà per vera e pubblicherà anche nella sua Short Cronicle),[18] riducendo così di molto il periodo tradizionalmente accettato.[19]

 

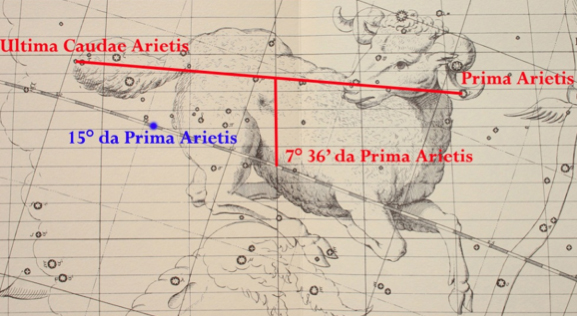
Immagine 2. Proiezione grafica del punto mediano tra Prima e Ultima Caudae Arietis sull'eclittica (in rosso) e sua differenza rispetto al punto mediano teorico a 15° da Prima Arietis, come avrebbero voluto molti dei critici di Newton (in blu) (elaborazione grafica su tavola di J. Flamsteed, Atlas coelestis, Londra, 1753).     

 
Occorre precisare che con punto mediano, Newton non intende, come alcuni critici coevi pensavano,[20] la posizione teorica basata sull'intera ampiezza convenzionale della costellazione (quindi a 15° dalla prima stella dell'Ariete, visto che, per convenzione, ogni costellazione zodiacale è ampia 30°) ma quella risultante dalla distanza tra le due stelle, Prima Arietis e Ultima caudae Arietis, poste agli estremi dell’asterismo principale (cioè a 7° e 36’):[21] una differenza di sette gradi e mezzo che, in anni, equivale a un intervallo di tempo di circa cinquecentotrenta.

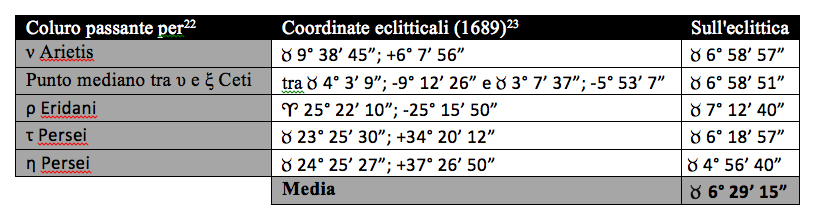
Tabella I. Tramite la descrizione del coluro equinoziale di Eudosso e le misurazioni di Flamsteed, Newton ottiene la longitudine eclitticale riferita al 1689 del punto d’intersezione tra coluro ed eclittica.
 

Oltre alla descrizione della sfera originaria, altre osservazioni antiche vengono da Newton utilizzate al fine d’individuare ulteriori datazioni storiche, partendo sempre dalle misure astrometriche dell’astronomo reale John Flamsteed. Tra queste spicca senz’altro la descrizione di Esiodo della levata eliaca della stella Arturo,[24] nell’interpretazione newtoniana. In questo caso il metodo utilizzato non è descritto esplicitamente nella Chronology, cosicché si deve fare affidamento ad alcune annotazioni presenti in un manoscritto precedente:

Esiodo ci racconta che sessanta giorni dopo il solstizio invernale la stella Arturo sorgeva proprio al tramonto del sole. In quei giorni, e per molto tempo ancora, i solstizi erano posizionati nel mezzo delle costellazioni del Cancro e del Capricorno e il loro spostamento non era conosciuto; l’apogeo del sole si trovava in B 24°. In questi sessanta giorni, più sei ore da mezzogiorno al tramonto, il sole si dovrebbe essere mosso dal solstizio invernale a L 0° 10’ e il punto opposto all’eclittica che sorge allo stesso momento di Arturo, dovrebbe essere in F 0° 10’. La latitudine di Arturo è 30° 57’ nord e l’elevazione del polo sul monte Helicon, vicino ad Atene, ove visse Esiodo, è 37° 45’, secondo quanto asserito da Claudio Tolomeo. Giovanni Battista Riccioli (Almagesto, VI, XX, prob. VIII) insegna come calcolare l’eccesso di longitudine di Arturo su quella del suo punto dell’eclittica, a esso opposto. Dai calcoli da me eseguiti risulta che tale eccesso sia di 11° 14’. Sommando questo valore a F 0° 10’, si ha la longitudine di Arturo in F 11° 24’. Quando il lembo superiore del sole è visibile, l’astro è ancora sotto l’orizzonte di 33’, essendo esso maggiormente elevato dall’effetto della rifrazione atmosferica; il suo centro è 16’ ancora più basso, in tutto 49’ sotto l’orizzonte. La parte dell’eclittica che si trova tra l’orizzonte e il centro del sole, risulta essere di 62’. Quando Arturo è visibile al suo sorgere, è anch’esso 33’ sotto l’orizzonte, sempre a causa della rifrazione; l’arco tra l’orizzonte e la stella parallela alla latitudine è di 41’ e ¼. Sommando i 62’ e i 41’ e ¼, si ottengono 103’ e ¼, che vanno poi aggiunti alla longitudine di Arturo sopra indicata, ottenendo il risultato finale di F 13° 7’ e ¼. La longitudine di Arturo al tempo della spedizione degli Argonauti era F 13° 24’ 52” [cioè la posizione ricavata sottraendo i 36° 29’ alla posizione osservata da Flamsteed, nel 1689, di G 19° 53’ 52”, ndt], come sopra. La differenza di 17’ 37” è così ridotta da essere praticamente impercettibile agli antichi astronomi […].[25]

I calcoli di Newton, quindi, dimostrerebbero la precedenza di qualche decennio della spedizione degli Argonauti rispetto all’osservazione di Esiodo, entrambe comunque successive alla morte di Salomone (980 a.C.); ma ciò non chiarisce la discrepanza di circa cinquant’anni (17’ e 37” corrispondono a circa vent’anni) tra i risultati riportati in questo manoscritto e i risultati dichiarati nell’opera edita, che coinciderebbero con quanto Newton deduce in altri passi dello stesso Esiodo (cioè che il poeta visse una generazione, cioè circa trentatré anni, dopo la guerra di Troia, quindi due, cioè circa sessantasei anni, dopo la spedizione degli Argonauti).[26] Nonostante la mole considerevole di materiale autografo newtoniano conservatisi, rimane arduo stabilire con sicurezza se altri e diversi calcoli siano stati effettuati tra questo manoscritto e la redazione ultima della Chronology, ma nasce spontaneo il sospetto che l’oscurità con la quale Newton espone questi risultati[27] nasconda qualche incertezza. Non appare un caso, in effetti, che questo argomento non sia citato nella lista, redatta informalmente dallo stesso Newton, che sintetizza gli elementi originali del suo sistema cronologico.[28] Anche le osservazioni astronomiche di Ipparco, Talete, Achille Tazio e Columella completano la sequenza di posizioni astrometriche che Newton rintraccia nella mole monumentale di fonti da lui lette e analizzate e che utilizza per datare altrettanti eventi storici.[29]
    Nell'analisi della struttura e della datazione del monumento funebre di Amenofi, descritto da Ecateo e distrutto poi da Cambise,[30] Newton unisce astronomia e "archeologia", seppur mediata da narrazioni tratte da fonti storiche. Pur nella diffidenza nei confronti dei reperti archeologici e, più in generale dell'antiquaria,[31] Newton si occupò a più riprese della struttura architettonica di alcuni monumenti antichi (alcuni dei quali già scomparsi alla sua epoca e ricostruiti tramite fonti indirette), convinto di trovare all'interno di essa proporzioni e configurazioni simboliche in grado di rivelare informazioni nascoste, in modo più o meno consapevole, da poter quindi decifrare.
    Durante il regno di Amenofi, gli Egizi determinarono con precisione l’equinozio primaverile e collocarono in tale giorno l’inizio del loro anno: secondo Newton, ciò sarebbe evidente dal fatto che essi collocarono un cerchio di 365 cubiti di circonferenza, coperto sul lato superiore con una placca d’oro, divisa in 365 parti uguali, per rappresentare tutti i giorni dell’anno; ogni parte aveva incisi il giorno dell’anno e le levate e i tramonti eliaci delle stelle riferite al giorno corrispondente. Se ne deduce, quindi, che fu Amenofi, quand'era ancora in vita, a stabilire l'aggiunta di cinque giorni intercalari all'anno lunisolare, fissando il suo inizio proprio nell'equinozio di primavera.[32] Nel tempo, questo tipo di anno s’introdusse in Caldea e costituì il modello per l’anno di Nabonassar: per tale anno e per quello degli egizi, l’inizio fu fissato nello stesso giorno, chiamato Thoth, che nel principio del regno del sovrano babilonese (747 a.C.) cadeva il 26 febbraio, cioè trentatré giorni e cinque ore prima dell'equinozio primaverile (il 29 marzo dell’antico calendario romano).[33] Seguendo l'equazione del moto solare, il Thot dell’anno si muove in modo retrogrado di trentatré giorni e cinque ore in centotrentasette anni,[34] quindi coincise con l’equinozio primaverile centotrentasette anni prima che l’era di Nabonassar iniziasse, cioè nell’884 a.C. Ecco così restituita, nella ricostruzione non proprio rigorosa e aderente al celebre suo motto, hypoteses non fingo, la data di edificazione del sepolcro di Amenofi e, quindi, della sua morte. La certezza con cui Newton propone i suoi risultati si può constatare da una sua stessa dichiarazione, presente nell'introduzione alla Chronology: egli scrive, infatti, di aver potuto sbagliare al massimo “di cinque o dieci anni, talvolta anche di venti, ma non di più”:[35] egli, quindi, accredita al proprio lavoro un grado di verità comparabile a quello da egli stesso raggiunto nell’ambito della filosofia naturale (che, diversamente da quello cronologico, gli assicurò, giustamente, l'immortalità).
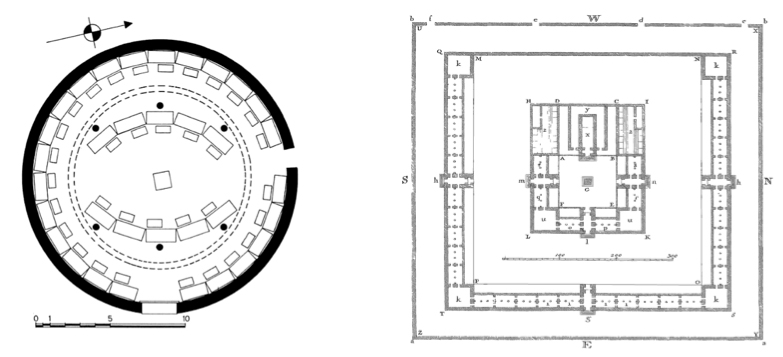
    Le incursioni newtoniane nell'ambito della ricostruzione teorica di edifici antichi, talvolta già scomparsi, come si è già accennato, sono dovute alla convinzione che le loro strutture architettoniche fossero portatrici di un messaggio occulto fortemente simbolico. È il caso degli antichi edifici sacri denominati, al tempo di Newton, pritanei: essi avrebbero rimandato all'antica idea eliocentrica della struttura dell’universo (a cui aderì, com’è noto, Aristarco di Samo che riprese il sistema del fuoco centrale di Pitagora il quale a sua volta, secondo Newton, avrebbe ricevuto frammenti della prisca sapientia dallo stesso Mosè), prima che fosse corrotta dal geocentrismo tolemaico; l’architettura di tali edifici, infatti, prevedeva un fuoco centrale intorno al quale vi era uno spazio sacro circolare in cui si riunivano i membri del consiglio degli anziani (in realtà era la tholos ad avere struttura circolare, non il pritaneo come si riteneva a quei tempi)[36]: questa disposizione avrebbe dovuto richiamare la disposizione dei pianeti intorno al Sole (v. Immagine 3).[37]
    In un manoscritto databile intorno ai primi anni novanta del Seicento, Newton accenna ai ruderi del sito di Stonehenge, riferendosi alla comune struttura, quella dei pritanei, che avrebbero avuto i primi edifici religiosi e politici nell’antichità, in ogni parte del mondo:
    In Inghilterra, vicino a Salisbury, vi è un rudere chiamato Stonehenge che sembra essere un antico pritaneo. Si tratta, infatti, di un’area circolare con due file di enormi pietre con passaggi su tutti i lati per consentire alle persone di entrarvi e uscirvi. Si dice che vi sono alcuni ruderi della stessa forma e struttura in Danimarca. E’ da ritenersi che i templi di Vesta di tutte le nazioni, come quelle dei Medi e dei Persiani, erano al principio nulla più che aree circolari aperte con un fuoco in mezzo, finché agglomerati e città unite sotto un consiglio comune ne costruirono altri sontuosamente. In Irlanda uno di questi fuochi si conservò fino ad anni recenti dai monaci di Kildare sotto il nome di fuoco di Santa Brigida e il cenobio era chiamato “la casa del fuoco”. Lo stesso culto era in uso anche tra i Tartari, come Guglielmo di Rubruck e Giovanni Plancarpinio ci informano. E gli Indiani ancora mantengono questo fuoco sacro e lo chiamano Homan. Benjamin Tudensis ha trovato lo stesso culto del fuoco in alcune isole delle Indie Orientali che egli chiama Chenerag. Viaggiatori riportano la stessa cosa per la Cina. Bardasane, un Siro che visse durante il dominio dell’imperatore Marco Antonino, scrive che “tra i Seri (o abitanti della Cina) il culto delle immagini era proibito da una legge e in tutta quella grande regione non vi era un tempio da vedere”. Da ciò io credo di dedurre che i Cinesi ancora a quei tempi avevano soltanto pritanei aperti senza edifici, come erano in uso tra i Medi o i Persiani.[38]

   

Qui è chiara l’influenza del neoplatonico di Cambridge, maestro di Newton, Henry More; la stessa influenza ravvisabile nell'intero capitolo dedicato al tempio di Gerusalemme, inserito nella Chronology. More definisce, infatti, il metodo che prevede l'interpretazione delle strutture architettoniche degli antichi edifici sacri, in particolare del tempio di Gerusalemme, come metafore mistiche e simboli esse stesse, come la ricerca di “[…] uno schema profetico assai frequente, specialmente nell’Apocalisse, che parla di affari della chiesa cristiana attraverso l’indicazione di nomi e con allusioni a quei luoghi, persone, cose riguardanti l’antichità degli Israeliti e del popolo degli Ebrei che assumono un significato mistico e spirituale”[39]. Lo stesso More cita San Paolo, secondo il quale per gli Ebrei “le immagini hanno qualche potenza in se stesse” (1Cor, X, 19). Con questi presupposti, Newton tenta quindi di riprodurre, anche graficamente, la pianta del tempio di Gerusalemme, secondo la descrizione che ne fa Ezechiele (Ez, XL), utilizzando come base di lavoro la versione della Bibbia di re Giacomo e comparandola con le altre versioni, compreso il testo masoretico (v. Immagine 4). L’idea della centralità del rito e del culto ebraici per la miglior comprensione della Rivelazione e della letteratura sapienziale, comportò per Newton la necessità di un'approfondita conoscenza della religione ebraica, attuabile in maniera proficua solo tramite la padronanza del linguaggio originale della Bibbia, raggiunta probabilmente già a metà degli anni settanta del XVII secolo.

Alessio Miglietta

 NOTE

[2] I. Newton, Philosophiæ Naturalis Principia Mathematica, Londra, 1687, p. 470 (lib. III, prop. XXXIX, prob. XIX e XX).
[3] Cfr. J. Flamsteed, Historia Celesti Britannica, London, 1725, II e id., Stellarum Inerrantium Catalogus Britannicus, ad Annum Christi Completum, 1689, London, 1725. Nelle precedenti stesure manoscritte della Chronology, Newton si affidò alle misure di Hevelius (Prodromus astronomiae, Danzig, 1690).
[4] Cfr. Clemente di Alessandria, Gli stromati, I, 15 e Oxford, New College Library, Keynes Ms 361(3), f. 194r.
[5] Cfr. N. Conti, Mytologiae sive explicationis fabularum, IV, 12.
[6] Cfr. D. Laerzio, Vite dei filosofi, I, proemio.
[7] La sfera celeste era rappresentata dagli astronomi antichi sia tramite proiezione su un piano, sia in tre dimensioni da un globo, solitamente in terracotta o metallo, sul quale tracciavano costellazioni e coordinate celesti, risultati dalle loro osservazioni dirette. Cfr. F. Cumont, Zodiacus, tr. it. L. Perilli, Lo Zodiaco, Milano, 2012, pp. 28-35.
[8] Le costellazioni della Chioma di Berenice (dedicata alla regina Berenice II, sposa di Tolomeo III Evergete ) e di Antinoo (introdotta da Tolomeo in onore dell’amante dell’imperatore Adriano, oggi scomparsa) che sarebbero, però, eccezioni confermanti la regola. Cfr. I. Newton, Chronology of Ancient Kingdoms Amended, London, 1728, p. 85.
[9] Storia naturale, VII, 56.
[10] Biblioteca, I, 9, 25.
[11] Cfr. Suida, in Aυαγαλλις.
[12] Omero, Odissea, VI, vv. 115-116. Un’ottica critica su questo aspetto dell’esegesi newtoniana, più che nei diversi testi inglesi e francesi risalenti agli anni immediatamente successivi alla pubblicazione della Short Chronicle e della Chronology, la si trova nello splendido lavoro del giovane Leopardi. Cfr. G. Leopardi, Storia dell’astronomia, cap. 1.
[13] Cfr. Ipparco di Nicea, Commentario su Arato di Soli, Fenomeni, II, 3.
[14] La stella Prima Arietis corrisponde alla lettera γ della classificazione di Bayer e non α, come viene in genere erroneamente indicato, v. ad esempio L. Pierce e M. Pierce in I. Newton, Newton's Revised History of Ancient Kingdoms: A Complete Chronology, Green Forest, 2009, p. 39. Cfr. J. Flamsteed, Historia celesti Britannica, cit., II, pp. 7-10 e 13-15; J. Flamsteed, Stellarum Inerrantium Catalogus Britannicus, ad Annum Christi Completum, 1689, cit., p. 1. V. anche Immagine 2.
[15] Stella priva di catalogazione di Bayer, è chiamata “I ad τ” Arietis da Flamsteed e corrisponde alla “Ultima seu Tertia Caudae” del Catalogus stellarum fixarum di Johannes Hevelius (1690), utilizzato dallo stesso Newton, prima di entrare in possesso delle misure di Flamsteed. Cfr. J. Flamsteed, Stellarum Inerrantium Catalogus Britannicus, ad Annum Christi Completum, 1689, cit., p. 1; F.E. Manuel, Isaac Newton Historian, cit., pp. 71 e 82 e J. Hevelius, Prodromus astronomiae, Danzig, 1690, p. 156.
[16] Non rimane traccia in alcun manoscritto del procedimento utilizzato da Newton. Un'ipotesi sul metodo di calcolo è formulata in J.Z. Buchwald e M. Feingold, Newton and the Origin of Civilization, Princeton, 2012, pp. 459 e ss.
[17] Il cerchio passante per i poli e per gli equinozi, e quello passante per i primi e per i solstizi, si dicono coluri. Newton si riferisce al sistema di coordinate celesti dette eclitticali, cioè al sistema che ha come piano fondamentale l’eclittica, ovvero la linea immaginaria che attraversa la sfera celeste e che descrive, interpolandolo, il percorso apparente del sole, rispetto alle stelle fisse, durante l’anno.
[18] Cfr. I. Newton, Chronology of Ancient Kingdoms Amended, cit., pp. 88 e ss.
[19] Denis Petau, ad esempio, collocava la spedizione nel 1263 a.C. Cfr. D. Petau, Abrégé chronologique de l'histoire universelle sacrée et profane, v. IV, Paris, 1715, p. 29.
[20] Cfr. N. Fréret, Défense de la chronologie fondée sur les monuments de l’histoire ancienne, contre le système chronologique de M. Newton, Paris, 1758.
[21] Cfr. I. Newton, Remarks on the Observations made on a Chronological Index of Sir Isaac Newton, translated into French by the Observer, and published at Paris, in Philosophical Transactions of the Royal Society, London, 1725, XXXIII, 399, pp. 317-318; Cambridge, King’s College, Keynes Ms. 138 e Gerusalemme, Jewish National and University Library, Yahuda MS. 27, ff. 1v e 5r.
[22] Cfr. Ipparco di Nicea, Commentario su Arato di Soli, Fenomeni, I, 2.
[23] Cfr. J. Flamsteed, Stellarum Inerrantium Catalogus Britannicus, ad Annum Christi Completum, 1689, cit., pp. 2, 25, 39, 40.
[24] Cfr. Esiodo, Le opere e i giorni, vv. 564-567 e D. Petau, Variarum dissertationum in Uranologion sive sistema variorum authorum, cit., pp. 90 e ss.
[25] Gerusalemme, National Library of Israel, Ms 25.1a, f. 1r. Cfr. anche Oxford, New College Library, Keynes Ms 361(3), f. 92r. e J. Flamsteed, Stellarum Inerrantium Catalogus Britannicus, ad Annum Christi Completum, 1689, cit., p. 50.
[26] Tramite l’identificazione di Anfidamante, citato da Esiodo, con l’omonimo partecipante alla guerra di Troia e considerando la cosiddetta quinta età, nella quale l’antico autore dichiarava di vivere, successiva a questa guerra. Cfr. Esiodo, Opere e giorni, vv. 648-662 e vv. 174-175; Omero, Iliade, XXIII, v. 87.
[27]Cfr. F.E. Manuel, Newton Historian, cit., p. 65.
[28]Cfr. Oxford, New College Library, Ms. 361(2), f. 154v e 155r.
[29] Per un approfondimento rimando a I. Newton, Scritti storico-religiosi e filosofico-scientifici, a cura di D. Arecco e A. Miglietta, in corso di stampa.
[30] Cfr. D. Siculo, Biblioteca storica, I, 49 ed Ecateo in ibidem, I, 32.
[31] Newton ebbe a dire che gli antiquari non erano altro che “amanti di bambole di pietra”. Cfr. J. Conduitt, Cambridge, King’s College, Keynes Ms. 130.07, f. 7v.
[32] Cfr. Strabone, Geografia, XII, 1; D. Siculo, Biblioteca storica, I, 50 e J. Marsham, Canon chronicus aegyptiacus, hebraicus, graecus, cit., p. 235.
[33] Secondo le fonti prevalenti, il giorno di Thot era fissato al sorgere eliaco di Sirio che all’epoca della sua inaugurazione coincideva approssimativamente con l’equinozio di primavera. Newton dice di considerare, per l’individuazione del giorno Thot, l’anno egizio di trecentosessantacinque giorni e non il ciclo canicolare. Cfr. Philosophical Transactions of the Royal Society, cit., XXXIII, 399, p. 320; Censorino, Sul giorno natale, 12; D. Petau, Opus de doctrina temporum, cit., pp. 649 e ss. e J. Marsham, Canon chronicus aegyptiacus, hebraicus, graecus, cit., p. 295.
[34] Cfr. G.G. Scaligero, De emendatione temporum, Geneva, 1629, pp. 391 e ss.
[35]Cfr. I. Newton, Chronology of Ancient Kingdoms Amended, cit., p. 8.
[36] Cfr. S.G. Miller, The Prytaneion. Its Function and Architectural Form, London, 1978, pp. 25-26.
[37] Cfr. B.J. Teeter Dobbs, Isaac Newton scienziato e alchimista. Il doppio volto del genio, trad. it. Roma, 2002, pp. 120-132; Gerusalemme, Jewish National and University Library, Yahuda Ms. Var. 1; Gerusalemme, Jewish National and University Library, Yahuda Ms. 41, f. 6.
[38] Yahuda Ms. 41, National Library of Israel, Jerusalem, Israel, f. 2v.
[39] H. More, Theological Works, London, 1708, p. 530. 

Bibliografia selezionata

ARECCO, DAVIDE
    I Fatti e le Idee. Scienza, religione e società nell’Inghilterra moderna, Genova 2007.
BUCHWALD, JED Z. E FEINGOLD, MORDECHAI
   Newton and the Origin of Civilization, Princeton, 2012.
DOBBS, BETTY JO TEETER
   The Janus Faces of Genius: The Role of Alchemy in Newton's Thought, Cambridge, 1991.
MANUEL, FRANCK E.
    Newton Historian, New York, 1968.
MAMIANI, MAURIZIO
    Introduzione a Newton, Roma – Bari, 1990.
MIGLIETTA, ALESSIO
   Teoria della materia e cosmologia in Isaac Newton: tra eredità stoica e nuova scienza, Genova, 2011.
   I segni del tempo. Le stelle nel mondo rurale e nell’immaginazione popolare, in «Anthropos & Iatria», 1, 2013, pp. 70-82.
   Da Zenone a Newton, in www.airesis.net.
NEWTON, ISAAC
    The Original of Monarchies, Cambridge, King’s College, Keynes Ms.146 (1702).
    Philosophiae Naturalis Principia Mathematica, London, 1726.
    Chronology of Ancient Kingdoms Amended, London, 1728.
    Trattato sull’Apocalisse, a cura di M. Mamiani, Torino, 1994.
     Scritti storico-religiosi e filosofico-scientifici, a cura di D. Arecco e A. Miglietta, in corso di stampa.
ROSSI, PAOLO
    Metamorfosi dell'idea di natura, Genova, 1999.
ROSSI, PAOLO ALDO
    I segni del tempo. Storia della Terra e storia delle nazioni da Hooke a Vico, Milano, 1979.
SARTORI, MARCO
   Voltaire, Newton, Fréret: la cronologia e la storia delle antiche nazioni in «Studi settecenteschi», Vol. 7-8, 1985-1986.

Sitografia

     NEWTON PROJECT: http://www.newtonproject.sussex.ac.uk/prism.php?id